Coq is a proof management system that provides a formal language to write mathematical definitions, executable algorithms, and theorems together with an environment for semi-interactive development of machine-checked proofs. This tutorial will guide you through the process of installing Coq on Windows, Mac, and Linux, and then how to write a simple proof using coqtop. coqtop is the Read-Eval-Print Loop (REPL) for Coq. It allows you to interactively develop proofs. If you come from Haskell, you can think of Coq like GHC and coqtop like GHCi.

Installing Coq

• Installing Coq on Windows

  • Download and run the Windows installer from the Coq website (https://coq.inria.fr/download).

• Installing Coq on Mac

  • The easiest way to install Coq on Mac is through Homebrew.
  • You can install Coq by running: brew install coq.

• Installing Coq on Linux

  • For Debian-based distributions like Ubuntu, use apt to install Coq.

    sudo apt install coq
    

  • For Red Hat-based distributions like Fedora, use dnf to install Coq.

    sudo dnf install coq
    

  • For Arch Linux-based distributions like Manjaro, use pacman to install Coq.

    sudo pacman -S coq
    

Writing a Simple Proof in Coq

Now, we aim to prove that 1 + 1 = 2 using Coq.

1. Let’s create a file named hello_proof.v and insert the following proposition that we seek to prove:

   Proposition one_plus_one_is_two : 1 + 1 = 2.
   

   If we attempt to compile our proof using coqc hello_proof.v, it will generate the following error, as expected:

   Error: There are pending proofs in file
   ./hello_proof.v: one_plus_one_is_two.
   

   That is because we have an unproven statement in our file. Now, lets try to prove this proposition interactively.

2. Start coqtop by running coqtop -load-vernac-source hello_proof.v in your terminal.

3. First, we need to enter proof mode by writing Proof., pressing enter, and then writing Show., followed by another enter, to view the current proof goal.

   Welcome to Coq 8.16.1
   
   one_plus_one_is_two < Proof.
   
   one_plus_one_is_two < Show.
   1 goal
   
     ============================
     1 + 1 = 2
   

   This is how it looks with with vim (top) and coqtop (bottom) in tmux: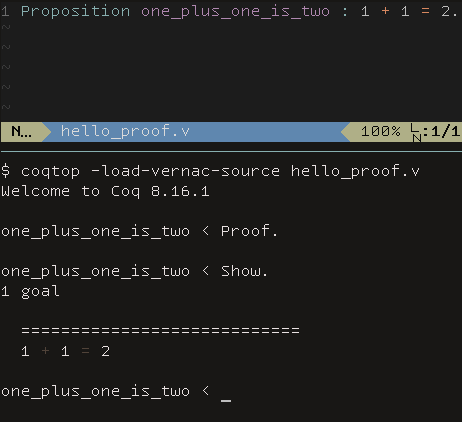

   

4. We have successfully loaded our proposition into coqtop and can now attempt to prove it using tactics. The first tactic I’d like to introduce is simpl. The simpl tactic reduces complex terms to simpler forms:

   one_plus_one_is_two < simpl.
   1 goal
   
     ============================
     2 = 2
   

5. As we can see, the simpl tactic has reduced our term 1 + 1 on the left side by evaluating it as 2. Now, it’s quite obvious that the term 2 = 2 is indeed true. We can solve the last goal with reflexivity, which is another basic tactic that solves the goal if it is a trivial equality, like in our case.

   one_plus_one_is_two < reflexivity.
   No more goals.
   

   After that we can write Qed. to end our proof and finish the proof mode.

   one_plus_one_is_two < Qed.
   

6. We can now put all the steps together into our hello_word.v file:

   Proposition one_plus_one_is_two : 1 + 1 = 2.
   Proof.
     simpl.
     reflexivity.
   Qed.
   

   and compile the proof with coqc hello_word.v.

Proof by Induction

1. Let’s prove that for all natural numbers, n - n = 0. In Coq, we can write this as follows:

   Proposition n_minus_n_equals_zero : forall n, n - n = 0.
   Proof.
     induction n.
   

   This starts the proof with the induction tactic. This setups two goals, the base case and the inductive step.

   2 goals
   
     ============================
     0 - 0 = 0
   
   goal 2 is:
    S n - S n = 0
   

2. The base case is trivial, with simpl. we have 0 = 0 and then just tell Coq that this is really the same reflexivity.

   1 goal
   
     n : nat
     IHn : n - n = 0
     ============================
     S n - S n = 0
   

3. Now, we are left with the inductive step S n - S n = 0. Let’s assume the proposition holds for n, and we show it holds for n + 1. simpl. applies simplification, reducing the expression S n - S n to n - n by definition of subtraction in Coq. rewrite IHn. uses the inductive hypothesis (IHn) to replace n - n with 0. Lastly, reflexivity. asserts that S n - S n simplifies to 0, which is true after the rewrite. Thus, the proof demonstrates that the proposition forall n, n - n = 0 holds true for all natural numbers n.

   Proposition n_minus_n_equals_zero : forall n, n - n = 0.
   Proof.
     induction n.
     - reflexivity.
     - simpl.
       rewrite IHn.
       reflexivity.
   Qed.
   

Conclusion

You might wonder how to come up with all these different tactics. Well, you can look them up, e.g., in the sheet from Cornell University, which is helpful: Coq Tactics Cheat Sheet, or examine various examples online. It requires some trial and error with simple proofs to become more proficient in proving with Coq. I can highly recommend the Software Foundations online book, which can be considered as the reference framework.

After successfully installing Coq and crafting a straightforward proof using the coqtop REPL, your journey into the meticulous world of formalizing mathematical proofs and programming language semantics is just beginning. Coq offers a robust toolkit for exploring these domains further. Keep exploring, and happy proving!