In the ΛCDM cosmological model, the Universe’s energy content is dominated by two unseen components – dark energy and dark matter – with only a small fraction composed of ordinary visible matter. This model assumes Einstein’s general relativity is the correct theory of gravity on cosmic scales and that the Universe is homogeneous and isotropic on large scales (the cosmological principle). Within this framework, ΛCDM posits the following key components.

Dark energy represents a mysterious form of energy inherent to space itself (often thought of as vacuum energy) that causes a repulsive effect, driving the accelerated expansion of the Universe.^[2][3] It is mathematically modeled by the cosmological constant Λ, a term in Einstein’s equations with an unusual property: it has negative pressure (an outward push) that counteracts gravity on large scales, leading to speeding-up of cosmic expansion.^[15] One can imagine dark energy as an extremely diffuse, invisible “fuel” permeating space – as space expands, more of this fuel appears, pushing space to expand even faster. In the ΛCDM model, dark energy is estimated to comprise roughly 2/3 of the universe’s total energy content.^[4][5] Importantly, dark energy is uniform (the same everywhere) and does not clump into structures; instead, it becomes dominant only at the largest scales and later times. It does no work on small scales (e.g. within galaxies), but across the vast reaches of intergalactic space its anti-gravity effect accumulates. This component was introduced to explain observations of accelerating expansion and is often considered equivalent to a constant energy of the vacuum.^[16] (Notably, “dark” simply means we do not yet know its nature – as scientists candidly admit, “we don’t know what dark energy is” beyond its effects.)

Cold dark matter is a form of matter that does not emit, absorb, or reflect light – invisible “matter” detected only via gravity.^[17] The term “dark” indicates that these particles interact extremely weakly (if at all) with light or ordinary matter, and “cold” means the particles moved at slow (non-relativistic) speeds in the early universe.^[14] Because they were sluggish, cold dark matter particles could clump together even in the young universe, providing gravitational seeds for structure formation. One can think of cold dark matter as an invisible scaffold or glue: it forms massive, diffuse halos in which galaxies and clusters develop, holding them together by gravity. Unlike normal matter, CDM cannot radiate away energy (it’s “dissipationless”), so it cannot collapse into small dense objects or disks; it mainly forms large spherical halos of various sizes. Cold dark matter makes up roughly a quarter of the Universe’s energy content.^[4] Its presence explains a range of otherwise puzzling observations – for example, galaxies rotate faster in their outskirts than visible matter alone can account for, and galaxy clusters have far more gravity (binding them) than the visible galaxies and gas can supply. Those phenomena require a substantial amount of unseen mass. Leading hypotheses for CDM include new subatomic particles (e.g. WIMPs – weakly interacting massive particles, or axions), or even primordial black holes.^[19] However, these particles have not yet been directly detected, highlighting that CDM is an inferred component. In ΛCDM, cold dark matter’s role is crucial: it provides the gravitational wells into which ordinary matter falls to form galaxies and structure, and it does so in a “bottom-up” way (small clumps of dark matter merge into larger ones over time).^[14] This hierarchical clustering is a hallmark of the model and matches observed patterns of galaxy formation.

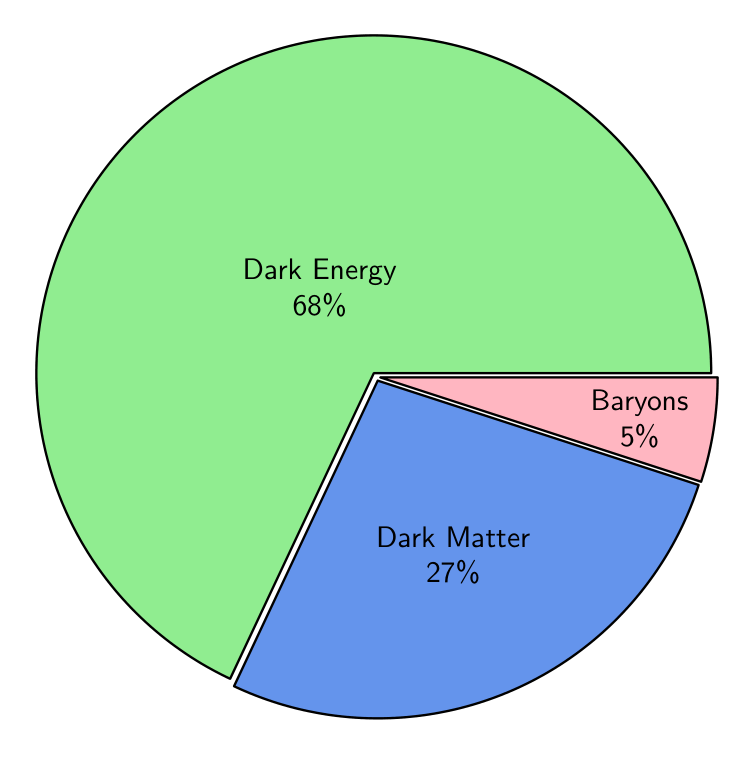
Baryonic matter is the familiar material composed of atoms – protons, neutrons, electrons – that forms stars, planets, gas clouds, and living beings. In ΛCDM, baryonic (or “luminous”) matter constitutes only about 5% of the Universe’s total energy density.^[4] It’s often said that everything we directly see – all the glowing stars, glowing nebulae, and visible galaxies – is just the tip of the cosmic iceberg. Despite its small overall fraction, baryonic matter is vitally important as it forms the visible structures of the cosmos. Baryons can radiate energy (e.g. as light or heat), which allows them to cool and collapse into disks and stars within the gravitational potential wells provided by dark matter halos. Thus, while dark matter provides the scaffolding, baryonic matter provides the “bricks and mortar” of galaxies. Baryonic matter interacts via electromagnetism, nuclear forces, and gravity – leading to the rich physics of stars and chemistry – but on cosmological scales its density was too low to create the Universe’s large-scale structure without the aid of dark matter’s additional gravity. Importantly, the ΛCDM model includes all three components (Λ + CDM + baryons) in a flat, expanding spacetime. The concordance proportions, based on modern observations, are approximately Λ ~ 68%, CDM ~ 27%, and baryonic matter ~5% by energy density, with a negligible remainder in relic radiation (e.g. the cosmic microwave background and neutrinos).^[4] These numbers paint a striking picture: the bulk of the cosmos is governed by ingredients we cannot directly see, and ordinary matter plays only a supporting (though observable) role. The precise amount of baryonic matter is constrained by both CMB observations and Big Bang nucleosynthesis calculations.^[7][8]

Historical Development and Observational Evidence

Emergence of the ΛCDM Model: The ΛCDM paradigm arose in the late 20th century as a unifying solution to reconcile disparate cosmological observations.^[15] In earlier decades, cosmologists struggled to agree on the Universe’s composition. By the 1980s, the Big Bang theory was well-established (bolstered by the 1965 discovery of the cosmic microwave background), and evidence for unseen “dark” matter in galaxies was mounting.^[13] However, a single coherent model was elusive. For example, Einstein’s cosmological constant Λ had been proposed as a theoretical tweak to gravity back in 1917, then largely abandoned, only to be resurrected decades later when observations hinted it might be needed after all.^[16] Dark matter had entered the scene through observations like Fritz Zwicky’s 1933 report of missing mass in galaxy clusters and Vera Rubin’s seminal work in the 1970s showing galaxies’ rotation curves were flat – implying a halo of invisible mass surrounding each galaxy.^[19] Meanwhile, the theory of cosmic inflation (developed in the early 1980s) predicted a nearly flat Universe (total energy density very close to the critical density).^[14] If the Universe was indeed flat as inflation suggested, the known forms of matter (baryons plus dark matter) seemed to fall short of providing 100% of that critical density – a clue that an additional energy component (like Λ) might exist.^[15]

Throughout the 1980s and early 1990s, cosmologists explored models with cold dark matter to explain how galaxies formed out of the tiny primordial ripples seen in the CMB. A Cold Dark Matter dominated universe (CDM) with critical density was initially favored, but it ran into difficulties.^[17] Simulations with only matter (no Λ) could form large-scale structures, but they tended to require a slower expansion rate (low Hubble constant) than observations indicated, and they struggled with certain clustering data. Observational hints also began to suggest that the total matter (dark + normal) was only ~20–30% of critical density, not 100%.^[15] This tension set the stage for a “missing energy” component.

The breakthrough came in the late 1990s: distant supernova observations in 1998 revealed the Universe’s expansion is accelerating, directly implying a dominant repulsive energy like Λ.^[2][3] Two independent teams (the Supernova Cosmology Project and the High-Z Supernova Search Team) observed dozens of Type Ia supernovae – standard candle explosions used to measure cosmic distances – and found they were fainter (more distant) than expected in a decelerating universe. In other words, expansion had sped up over time. This astonishing discovery was the first direct evidence for a positive cosmological constant (dark energy), and it cemented the need for Λ in the model. The result, announced in 1998, led to the concept of a “double dark” cosmos: one dark sector providing gravity (CDM) and another driving acceleration (dark energy).^[15] The formerly controversial ΛCDM model rapidly became the “concordance model” after 1998, because it seemed to neatly concord (bring into agreement) a host of prior inconsistencies.^[16] Following the supernova evidence, a cascade of observations in the late 1990s and 2000s confirmed and refined the ΛCDM model.

Cosmic Microwave Background (CMB)

The CMB – the faint afterglow of the Big Bang, dating to about 380,000 years after the initial expansion – provided a wealth of precision data. The first detection of tiny anisotropies (temperature ripples) in the CMB by the COBE satellite in 1992 hinted at the seeds of structure formation.^[9] Later, balloon-borne experiments like BOOMERanG (2000) measured the CMB’s first acoustic peak, indicating that the Universe’s geometry is flat, consistent with Ω_total ≈ 1. This was a critical test: BOOMERanG found the total matter-energy density is very close to 100% of the amount needed for a flat universe, supporting the presence of Λ since matter alone only contributed ~30%.^[13] The Wilkinson Microwave Anisotropy Probe (WMAP, 2001–2010)^[11][12] and later the Planck satellite (2009–2013)^[4][5] mapped the CMB across the whole sky with high precision. Their data brilliantly fit the ΛCDM model’s predictions, measuring the fractions of dark matter, dark energy, and baryons to within a few percent. For example, Planck’s results in 2013–2018 pinned down the dark energy density around 68% and matter ~32% (consistent with earlier supernova and galaxy data) with uncertainties of only a percent or so.^[4][5] The pattern of multiple acoustic peaks in the CMB power spectrum – essentially a snapshot of the primordial universe’s plasma oscillations – matches the ΛCDM model when it includes ~5% normal matter, ~25% cold dark matter, and ~70% Λ, validating the model’s basic ingredients. The CMB also provides an age of the universe (~13.8 billion years) that agrees with ΛCDM and resolves earlier puzzles (with Λ, the universe is older, alleviating the 1990s “old star” paradox where some globular clusters appeared older than an Einstein-decelerating universe allowed).^[13][18] Overall, high-resolution CMB observations are often cited as a “rosetta stone” for cosmology – and their message is that a ΛCDM cosmology is an excellent fit to our universe.

Large-Scale Structure and Galaxy Surveys

The distribution of galaxies on cosmic scales – mapped by redshift surveys such as the Sloan Digital Sky Survey (SDSS) and the 2dF Galaxy Redshift Survey – provided another pillar of evidence.^[6] These surveys, around 2000–2005, mapped the three-dimensional positions of hundreds of thousands of galaxies. They revealed a “cosmic web” of filamentary structure and voids that grew over billions of years from initial fluctuations.^[14] ΛCDM simulations (N-body computer simulations of dark matter plus gas physics) naturally produce the same cosmic web pattern, supporting the model qualitatively.^[13] More quantitatively, the surveys detected a subtle but important feature: the baryon acoustic oscillation (BAO) scale. BAOs are a relic imprint of sound waves in the early plasma; in the present universe they appear as a preferred clustering scale (~500 million light years) at which galaxy pairs are slightly more likely to be separated. In 2005, astronomers observed this BAO “standard ruler” in the clustering of galaxies at exactly the scale ΛCDM predicted.^[6] The BAO measurement provides an independent confirmation of the cosmic expansion history consistent with a dark energy-dominated universe. Galaxy cluster counts and gravitational lensing surveys likewise are in line with ΛCDM’s matter distribution.^[5] Notably, the 2dF survey in 2001 measured the matter density Ω_m ≈ 0.25, which, when combined with the flatness requirement (Ω_total ≈ 1 from CMB), strongly indicated Ω_Λ ≈ 0.75 – precisely what the supernova data had suggested.^[6] Thus multiple independent lines of evidence “triangulated” on the same answer. The large-scale structure data also show that structure grows hierarchically (small galaxies are common and form early, massive clusters form later by mergers), which is a pattern expected in a cold dark matter scenario.^[14]

Type Ia Supernovae (Accelerating Expansion)

The 1998 discovery of accelerating expansion via distant Type Ia supernova observations is often considered the “defining moment” for ΛCDM.^[2] Type Ia supernovae serve as standard candles – all having nearly the same intrinsic brightness – so by comparing their apparent brightness and redshift, astronomers can trace how the expansion rate has changed over time. The supernova teams found that distant supernovae (light from ~5–7 billion years ago) were dimmer than expected for a universe slowing down – implying instead that expansion has sped up (the galaxies were farther away than a decelerating model would predict).^[3] This result was surprising, since prior to 1998 most expected gravity’s pull would be slowing the expansion. The immediate interpretation was that some form of repulsive energy (Λ) presently dominates the cosmos.^[15] Subsequent supernova experiments with larger samples have reinforced this conclusion, placing the dark energy fraction around 70% of the energy budget.^[4][5] Together with the CMB and BAO findings, supernovae evidence established the concordance values of (Ω_m ~0.3, Ω_Λ ~0.7) that define ΛCDM.^[15] This breakthrough was deemed so fundamental that the leaders of the two supernova teams were awarded the 2011 Nobel Prize in Physics.

In summary, by the early 2000s the ΛCDM model became the standard cosmological model – often referred to as the “Standard Model of Cosmology” – because it successfully explained a wide range of observations with a simple set of ingredients. It provides a coherent history of the universe from a hot Big Bang, through the formation of structure, to an accelerating present-day expansion. The combination of evidence from the CMB, large-scale galaxy clustering, and distant supernovae – sometimes called the “Cosmic Trinity” – all point to the same cosmic recipe: a flat universe with ~5% normal matter, ~25% cold dark matter, ~70% dark energy.^[4][5][15] No alternative model so far has matched the breadth of ΛCDM’s observational successes.

Physical Interpretation of Cold Dark Matter

A central feature of ΛCDM is that the dark matter is cold. In this context, “cold” does not refer to temperature in the everyday sense, but to particle velocity in the early universe.^[19] Cold dark matter particles move slowly (typically much slower than light) during the epoch when galaxies and large-scale structures began forming.^[14] This has profound consequences for how structure forms over cosmic time. To understand this, consider how different types of dark matter would influence the growth of structures (like galaxies, clusters, and the cosmic web of matter).^[13]

Cold Dark Matter

Being slow-moving and massive, cold dark matter can clump on small scales early on. In the primordial universe, regions that were slightly denser than average could gravitationally attract CDM particles, and because those particles weren’t racing around at near light-speed, they tended to stay and accumulate.^[13][14] This means small-scale fluctuations survive and grow.^[19] Over time, CDM’s gravity amplifies these seed fluctuations, drawing in gas and forming small protogalaxies first. Those small structures then merge hierarchically into larger ones – a “bottom-up” formation scenario.^[14] This hierarchical buildup is exactly what we see in observations: for instance, many tiny dwarf galaxies and sub-galactic fragments are observed, and large galaxies are built via mergers and accretion of smaller systems.^[6] ΛCDM simulations show innumerable small dark matter clumps (halos) merging to form galaxy halos and clusters, consistent with the abundance of dwarf galaxies (which are thought to be the visible counterparts of some of those small halos). CDM also has effectively no pressure or diffusion, so once a clump starts to form, it isn’t erased by dark matter particles dispersing – this helps the growth of dense halos. In short, cold dark matter provides a gravitational scaffolding on all scales: from the mass of small dwarf galaxies (~10^7–108 solar masses) up to the largest clusters (~10^15 solar masses).^[19] Ordinary matter subsequently falls into these CDM clumps and forms stars and galaxies within them. The “coldness” is crucial; it’s why the model can explain the existence of small galaxies and early-forming structures.

Warm or Hot Dark Matter (contrasts)

If dark matter were “hot”, meaning composed of light, ultra-relativistic particles (such as hypothetical heavy neutrinos in the early universe), the story changes. Fast-moving particles zip out of small-scale density fluctuations, smoothing them out like wind blowing away small clumps of dust. In a hot dark matter scenario, tiny primordial clumps would not survive – only the largest overdensities could grow.^[13] Structure formation would then proceed “top-down”, with enormous supercluster-sized pancakes forming first and later fragmenting into galaxies.^[19] This top-down picture does not match what we observe; for example, we see dwarf galaxies that formed early, and the universe is far from smooth on small scales. Indeed, hot dark matter (e.g. if neutrinos dominated the mass) would yield very few small galaxies and would delay galaxy formation, in conflict with observations of early galaxies. Warm dark matter, an intermediate case (particles with speeds between cold and hot, such as a ~keV-mass sterile neutrino), would erase only the very smallest structures – damping out fluctuations below a certain size, but allowing intermediate and large-scale structure to form.^[1] Warm dark matter has been considered as a potential tweak to ΛCDM to address some small-scale problems (it could reduce the number of tiny halos, for instance).^[1] However, the canonical ΛCDM model uses cold dark matter because it best reproduces the full range of structures we see, from dwarf galaxies up to giant clusters.^[4][5] Cold dark matter’s ability to seed structure at all scales (except the very smallest, like sub-galactic scales below a million solar masses) makes it consistent with the rich hierarchy of the cosmic web.^[6]

Physically, what might cold dark matter be? Leading candidates include heavy, slow-moving particles that were born non-relativistic. A popular class of candidates are WIMPs (weakly interacting massive particles) – these would be particles with masses perhaps 100 times the proton mass, which interact via at most the weak nuclear force (hence “dark” to electromagnetism). In many theories, WIMPs would have been produced in the right abundance to be today’s dark matter. Another intriguing candidate is the axion, a very light particle with unusual properties that could act collectively like a cold Bose-Einstein condensate on cosmic scales. Even primordial black holes have been hypothesized (tiny black holes formed in the infant universe) – though most evidence disfavors them being a major component.^[19] The key point is that whatever dark matter is, it must be cold (slow-moving) by the time of galaxy formation and non-baryonic (not made of atoms). It also should be collisionless, meaning dark matter particles pass through each other and normal matter without collisions or interactions beyond gravity. These properties ensure dark matter forms the kind of halo structures that match observations. In ΛCDM, CDM halos start collapsing even during the so-called “Dark Ages” (before stars formed), creating a network of massive clumps. Gas then falls in and lights up as the first stars (“Cosmic Dawn”), marking the beginning of visible structure. Without cold dark matter, the universe would have a much harder time creating galaxies as early and as abundantly as it did.

In summary, cold dark matter provides the gravitational backbone for structure in the Universe. Its “coldness” (slow speed) means it can aggregate at small scales, enabling the hierarchical formation of galaxies and clusters that we observe. Warmer or hot varieties of dark matter would smear out structure and contradict the observed cosmic hierarchy. The success of ΛCDM in explaining the large-scale structure is largely thanks to the assumption of cold dark matter – an assumption that has so far passed all major observational tests, even as the true identity of the dark matter particle remains one of the biggest open questions in physics.

Success in Explaining the Universe

The ΛCDM model, despite its simplicity, has achieved remarkable success in describing the Universe’s history and large-scale properties. It is fully consistent with the framework of the Big Bang theory and incorporates general relativity as the governing theory of gravity. Essentially, ΛCDM is the Big Bang cosmological model enriched with just two additional ingredients (Λ and CDM) and initial conditions set by an inflationary epoch. With these, it provides a cohesive narrative for cosmic evolution that matches a host of observations across time and space.^[13] Some of the key triumphs of ΛCDM include:

Unifying Cosmic Expansion with Gravity

ΛCDM extends the classic Big Bang model by including dark energy, which allows it to account for the observed accelerating expansion of the Universe within general relativity.^[2] In a ΛCDM universe, for the first few billion years after the Big Bang, matter dominated and the expansion was slowing down (decelerating) due to gravity. But as space stretched and matter thinned out, the constant vacuum energy (Λ) eventually became dominant (around 5–6 billion years ago).^[4] Since Λ has repulsive gravity, the expansion switched to accelerating.^[2][3] This scenario naturally explains why we see distant galaxies speeding away faster now than in the past.^[16] It aligns with general relativity because Einstein’s equations with a positive Λ term predict exactly such behavior.^[15][16] Thus, ΛCDM elegantly blends Einstein’s gravity with cosmic expansion, requiring no modifications to GR – only the inclusion of Λ as Einstein originally allowed.^[15] It also implies the Universe will continue to expand forever, with acceleration, which matches the latest observations^[4] and solves the old puzzle of the Universe’s fate.^[18]

Explaining the Cosmic Microwave Background

The tiny temperature anisotropies in the CMB are a snapshot of the Universe at 380,000 years old, and ΛCDM provides a precise explanation for their statistical properties.^[5] In the model, prior to that time, the Universe was a hot ionized plasma of electrons, protons, photons, and a dash of dark matter. Acoustic (sound) waves oscillated in this plasma, driven by the interplay of gravity and pressure.^[14] ΛCDM, with a specific mix of 5% baryons and 25% dark matter, predicts a distinct pattern of peaks in the CMB’s angular power spectrum (essentially, the sizes of “hot and cold spots” on the sky).^[11] The first peak’s location reveals spatial flatness, the relative heights of the peaks reveal the baryon density and dark matter density, etc.^[12] Strikingly, the observed CMB power spectrum – measured by Planck and WMAP – matches ΛCDM’s predictions almost perfectly when using the best-fit parameters.^[11] For instance, the Planck satellite observed about seven acoustic peaks in the CMB temperature spectrum and several peaks in polarization spectra, all consistent with a six-parameter ΛCDM model.^[5] The existence of multiple peaks and their detailed shapes are a triumph for ΛCDM: it shows that the model correctly captures the physics of the early universe (including the roles of dark matter and baryons in those oscillations).^[4][13] Furthermore, ΛCDM is consistent with primordial element abundances: using the baryon density inferred from the CMB, the theory correctly predicts the abundances of hydrogen, helium, and deuterium produced in the first few minutes (Big Bang nucleosynthesis).^[8] For example, the model’s baryon density yields a deuterium abundance in excellent agreement with observations of ancient gas clouds.^[7] This cross-check, connecting the CMB (380,000 years post-Big Bang) to element formation (~3 minutes post-Big Bang), solidifies the model’s credibility.^[13]

Large-Scale Structure and Galaxy Formation

ΛCDM provides a robust framework for understanding how the Universe’s large-scale structure (the cosmic web of galaxies and clusters) formed from initial seeds. By assuming the primordial fluctuations were small and nearly scale-invariant (as predicted by inflation) and that dark matter is cold, ΛCDM accurately reproduces the hierarchical formation of structure.^[13] In simulations, tiny density perturbations grow under gravity into filaments and nodes (with dark matter collapsing first, forming halos).^[14] Ordinary gas follows, collecting in the gravitational potential wells of the dark matter halos, and eventually cooling and fragmenting into stars and galaxies.^[13][6] Over billions of years, small galaxies merge into bigger ones, and clusters of galaxies form at the intersections of filaments – all natural outcomes in ΛCDM. The observed galaxy cluster mass function (the number of clusters at different masses) and the clustering statistics of galaxies are in broad agreement with ΛCDM predictions across a range of redshifts.^[5] One particularly vivid success was the prediction of the baryon acoustic oscillation feature in galaxy clustering, which, as noted, was later discovered at the expected scale.^[13] The model also explains gravitational lensing measurements on large scales (how intervening mass bends light from distant galaxies): the lensing signal (e.g. in cosmic shear surveys) fits the ΛCDM distribution of dark matter. Additionally, the timeline of structure formation in ΛCDM is consistent with observations: for example, the model allows for the existence of protogalaxies and quasars at very high redshift (~within 300–400 million years after the Big Bang), which recent telescope observations (e.g. by James Webb Space Telescope) have indeed found.^[1][14] In ΛCDM, the first stars can form as early as z ~ 20–30 (around 100–200 million years after the Big Bang) once small dark matter halos (with masses of 10^5–106 solar masses) collect enough gas.^[13][14] This “cosmic dawn” scenario is supported by observations of early star formation and the reionization epoch (when the radiation from early galaxies reionized the primordial hydrogen).^[5] Thus, ΛCDM not only explains the present distribution of galaxies, but also provides a coherent picture of how galaxies evolve over cosmic time within dark matter halos.

Cosmic Timeline and Ages

The ΛCDM model yields a consistent age for the Universe (about 13.8 billion years) that reconciles with independent age estimates of the oldest stars and globular clusters.^[4] In older models without Λ, there was a nagging issue where the inferred Hubble constant and matter density would imply a universe younger than some stars.^[18] ΛCDM resolves this: the addition of dark energy slows down the past expansion less (and accelerates it late), giving a larger age.^[16] Moreover, the model elegantly incorporates an early inflationary period (to set up initial conditions)^[14] followed by a radiation-dominated era (when the universe was hot soup of particles and light), then a matter-dominated era (when structure formed under dark matter’s influence), and finally a dark energy-dominated era (today, causing acceleration). Each era’s key events – recombination (CMB decoupling), reionization, formation of the first galaxies, etc. – occur at times consistent with observations. For instance, ΛCDM predicts that recombination happens about 380,000 years after the Big Bang at a redshift ~1100, which is exactly what the CMB’s temperature and spectrum indicate.^[5] It predicts that by redshift ~z=0.5 (roughly 5 billion years ago) dark energy starts to dominate expansion, which aligns with the supernova evidence for when acceleration began.^[3] The model even correctly anticipated phenomena that were later observed: one example is the polarization of the CMB – ΛCDM predicted specific polarization patterns from the scattering of CMB photons during reionization, and those were measured in the 2000s, matching the model.^[12] All told, ΛCDM provides a single, overarching framework that ties together the origin of cosmic structure, the composition of the universe, the expansion history, and the cosmic microwave background.^[15] Its success is often summarized by the sentiment that “ΛCDM is extremely effective at explaining what we see in the universe, from the largest scales down to galaxy scales”.^[5] It is for this reason that ΛCDM is sometimes dubbed the “standard model of cosmology,” analogous to the standard model of particle physics in its scope and predictive power.^[18]

While ΛCDM is not literally a complete theory of everything (since we don’t yet know the microphysics of dark matter or dark energy), it beautifully encapsulates the cosmological behavior of the universe with only a handful of parameters.^[4][5] Those parameters (such as the densities of each component, the Hubble constant, the initial fluctuation amplitude, etc.) have been measured to high precision by experiments like Planck, leaving essentially a clear, consistent picture: a flat universe born in a hot Big Bang, structured by cold dark matter, and accelerated by dark energy.

Challenges and Limitations

Despite its many successes, the ΛCDM model is not without problems.^[1] Researchers are actively investigating a number of discrepancies and unresolved issues where the model’s predictions appear to conflict with certain observations.^[1][18] These challenges do not (so far) overturn ΛCDM, but they do highlight areas where our understanding is incomplete or new physics might be lurking. Key challenges and limitations include:

The Hubble Tension

One of the most discussed issues is a significant discrepancy in the measured Hubble constant (H₀) – the current expansion rate of the universe – depending on how it is measured.^[18] Using ΛCDM to extrapolate early-universe observations (primarily the CMB data from Planck) yields H₀ around 67 km/s/Mpc, whereas direct measurements in the local universe (using the cosmic distance ladder of Cepheid variable stars and Type Ia supernovae, by teams like the SH0ES collaboration) give H₀ around 73 km/s/Mpc. These two values differ by about 5–10%, and crucially, the uncertainty margins do not overlap – the disagreement has grown to a statistically significant tension.^[18] In essence, if ΛCDM (with the standard assumptions) is correct, both methods should yield the same H₀, so the persistent gap suggests something is off. This Hubble tension might indicate unrecognized systematic errors in one or both methods, but many experts suspect it could be a clue to new physics beyond ΛCDM. Possibilities include a small change in the early-universe physics (for example, an episode of “early dark energy” that alters the sound horizon in the CMB, or hidden interactions that affect the expansion rate). So far, no consensus solution exists, and the tension has only grown stronger with improved data. It’s a live issue: as Nobel laureate Adam Riess said, either there’s a series of unlikely errors or “there’s some kind of interesting new physics in the universe” causing the mismatch. The Hubble tension highlights that ΛCDM is not a perfect fit in all regimes, and it motivates new measurements (e.g., gravitational lens time delays, infrared distances) and theoretical tweaks to resolve the discrepancy.^[1]

Small-Scale Structure Problems

On the scale of individual galaxies and smaller, ΛCDM faces a set of challenges often referred to collectively as the “small-scale crisis.”^[1][19] These include:

• The cusp–core problem: Pure ΛCDM simulations of galaxy formation tend to produce “cuspy” dark matter halos – meaning the dark matter density is very high and sharply peaked at the centers of halos.^[1] However, observations of dwarf galaxies and low-surface-brightness galaxies often show a more “cored” (flat) inner density profile, with less dense centers than predicted. In other words, real galaxies don’t always exhibit the steep central gravity wells that ΛCDM (with cold, collisionless dark matter) would naturally create.^[19]

• The missing satellites problem: ΛCDM predicts that a Milky Way-sized halo should contain hundreds of smaller sub-halos (dark matter clumps), many of which could host dwarf satellite galaxies.^[1] Yet the actual Milky Way and Andromeda galaxies have only dozens of known dwarf satellites. There appears to be a shortfall of observed small galaxies compared to the vast number of sub-halos in simulations. Initially, it looked like ΛCDM over-produced small structures.^[14]

• The too-big-to-fail problem: In ΛCDM simulations, the largest sub-halos in a galaxy like the Milky Way are quite massive and dense – so massive that they should be able to form visible dwarf galaxies.^[1] Yet the satellites we observe aren’t orbiting in such extreme sub-halos; the most massive sub-halos seem to lack visible counterparts, implying a mismatch. They would be “too big to fail” to form stars by ordinary reasoning, and yet they failed to produce bright dwarfs.^[13]

Additionally, there are curiosities like the planarity of satellite galaxies, the dwarf satellites of the Milky Way and some other galaxies seem to lie on unexpected planes or orbits rather than in random distributions as naively expected in ΛCDM,^[1] and the tight correlations in galaxy scaling relations (e.g., the Tully-Fisher relation or the Radial Acceleration Relation) that some argue point to an underlying regularity not obviously predicted by CDM halos.^[19]

It’s worth noting that many of these small-scale issues might be resolved or alleviated by incorporating more realistic physics of ordinary matter (baryonic physics) into the simulations.^[13] For example, supernova explosions and stellar winds can inject energy into a small galaxy’s core and “puff up” the dark matter distribution, turning a cusp into a core. This feedback can also blow gas out of small halos, preventing many sub-halos from ever forming visible galaxies (addressing missing satellites and too-big-to-fail by essentially making some halos dark).^[1] Indeed, more recent high-resolution simulations that include star formation and feedback have had some success in reconciling ΛCDM with observed galaxy properties, suggesting these problems are not fatal to the model. Nonetheless, the small-scale discrepancies remain a topic of active research and debate.^[1] Some astronomers even consider alternative dark matter models (e.g., warm dark matter that naturally produces fewer small halos, or self-interacting dark matter that can create cores) or alternative gravity theories (like MOND) to better fit galaxy-scale data.^[19] So far, ΛCDM with baryonic feedback still appears broadly consistent with observations, but the details on sub-galactic scales are an ongoing puzzle.^[1]

Unknown Nature of Dark Components

ΛCDM is a phenomenological model – it describes what the Universe contains and how it behaves, but it doesn’t explain why those components exist or what they fundamentally are.^[18] Dark matter and dark energy remain mysterious.^[1] Decades on, no dark matter particle has been directly detected in laboratory experiments (despite sensitive searches with detectors in deep mines, particle collider experiments, etc.), and dark matter has only been observed indirectly via gravity.^[19] This raises the question: Is dark matter a particle at all, or could the theory of gravity itself be incomplete?^[1] The prevailing view is that dark matter is most likely some new particle, and experiments like LZ and XenonNT (underground detectors) are pushing to ever higher sensitivity. But the continued null results mean the possible properties of dark matter are being constrained into narrower windows, and some expected candidates (like simple WIMPs) have not shown up, which is a bit perplexing.^[19] Dark energy, on the other hand, is perhaps even more enigmatic. In ΛCDM it is simply a constant Λ – an intrinsic property of space – with no dynamics aside from making space expand faster.^[15][16] The measured value of Λ is astonishingly small in terms of fundamental physics units, which leads to the famous cosmological constant problem: theoretical quantum calculations of vacuum energy predict something like 10^120 times more vacuum energy than we observe – a colossal discrepancy.^[16][13] There’s no accepted explanation for why Λ is so tiny (yet nonzero), making it a profound fine-tuning problem. Moreover, we can’t yet distinguish whether dark energy is a true constant or perhaps a field that varies slightly in time (often called “quintessence” if it’s a dynamic field). Current data are consistent with a pure constant, but it’s hard to rule out slowly varying dark energy.^[4][5] For now, “dark energy” is essentially a placeholder term for “whatever is accelerating the expansion”. We have measured its effects but not its essence. This ignorance means ΛCDM, while empirically successful, leaves significant physics questions unanswered. In essence, the model begs deeper theory: What is Λ? Why that value? What is the dark matter particle and how did it form? These are outside the scope of ΛCDM itself.^[1]

Other Anomalies

There are a few other oddities under investigation. For example, detailed studies of the CMB by Planck have hinted at large-scale anomalies – e.g., a slight asymmetry in average temperature between opposite hemispheres of the sky, and the presence of a “Cold Spot” – which might suggest a violation of the simple statistical isotropy assumed in ΛCDM.^[4][5] These could be mere statistical flukes or foreground effects, but if real, they might require extensions to the model (perhaps in the inflationary initial conditions).^[14] Additionally, some measurements of the growth rate of structure (often parameterized by σ₈ or S₈, the amplitude of matter clustering) from weak gravitational lensing surveys (KiDS, DES, etc.) have come out a bit lower than the ΛCDM prediction from Planck CMB data.^[1] This is sometimes called the “S₈ tension” or a potential “growth tension”. It’s less significant currently than the Hubble tension, but it similarly raises the question of whether subtle new physics (like modified gravity or different neutrino properties) might be needed.^[1] None of these anomalies individually is strong enough yet to definitively break ΛCDM, but together they motivate a careful scrutiny of the model’s foundations.^[1]

It’s important to emphasize that no competing cosmological model has definitively supplanted ΛCDM – the data overall still favor this model’s basic framework.^[1][13] The approach in the community has been to tweak or extend ΛCDM rather than discard it wholesale. For instance, to address the Hubble tension, researchers have proposed variations like “early dark energy” (a temporary injection of energy in the early universe) or a change in the effective number of relativistic particles, etc., to try to reconcile early and late H₀ measurements.^[1][18] To address dark matter’s nature, physicists consider possibilities from supersymmetric particles to ultralight axions.^[19] As of now, ΛCDM with six or so free parameters still provides an excellent average description of cosmic observations. But the cracks at the edges are where cosmologists are focusing attention, as those may be hints of new physics beyond the standard model of cosmology.^[1]

The good news is that ongoing and upcoming surveys and experiments will subject ΛCDM to even more stringent tests.^[1] For example, the Dark Energy Spectroscopic Instrument (DESI) is in the process of mapping millions of galaxies in 3D, constructing the largest-ever map of the cosmos. By measuring the baryon acoustic oscillation scale and clustering of galaxies at various distances, DESI will tightly constrain the expansion history and the behavior of dark energy over time. It will also improve measurements of structure growth (testing the S₈ tension) and possibly reveal whether something like modified gravity is needed on large scales.^[1] Similarly, the Euclid satellite (launched by ESA in 2023) and the Vera C. Rubin Observatory’s Legacy Survey of Space and Time (LSST) will provide high-precision weak lensing and supernova data, further probing dark matter distribution and dark energy’s properties.^[18] These efforts, alongside particle experiments searching for dark matter, promise to either validate ΛCDM on ever finer scales or uncover deviations that could point to the next paradigm shift.^[19]

Conclusion

In conclusion, the ΛCDM model stands as a remarkably successful synthesis of our current knowledge about the Universe. It rests on a few foundational assumptions and ingredients that yield a wealth of accurate predictions, explaining everything from the cosmic microwave background to the distribution of galaxies. Its strengths lie in its simplicity and broad empirical support, while its weaknesses highlight the deep mysteries that remain – namely, the true nature of dark matter and dark energy, and some tensions in observational data. Like the standard model of particle physics, ΛCDM is likely an incomplete step toward a fuller understanding of the cosmos. But until a better theory comes along, ΛCDM continues to serve as the default model of cosmology, against which all new observations and ideas are compared. Future discoveries (whether resolving the Hubble tension, detecting a dark matter particle, or finding surprises in new surveys) will either refine this model or point the way to new physics, further illuminating the dark corners of our Universe.

References